3Dグラフィクスや最適化において,時系列順にならんだ姿勢の補間が必要になることがままある.この姿勢の補間に関して頻出する問題の割にどのように実装・利用したら良いかという記事が少ないように思うので備忘録的に書いておく.
姿勢の補間,特に回転成分の補間に関してはいくつも方法がある.例えば二つの回転をそれぞれオイラー角にして各軸の角度を補間する安直な方法やクォータニオンにしてSLERP補間する方法があるが,ここではジンバルロックなどの問題もなく複数姿勢間の補間に容易に拡張可能なExpmap/Logmapを使った補間を考える.
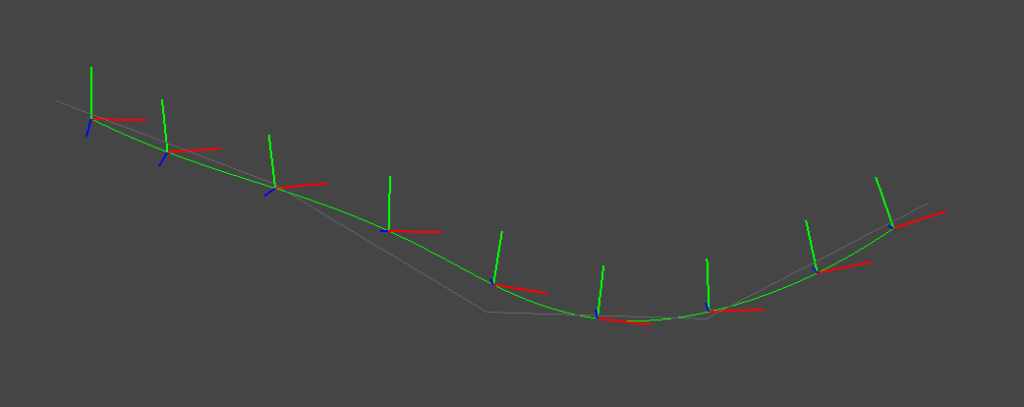
Expmap/Logmapを使った姿勢(SE3)のスプライン補間
Expmap/Logmapによる姿勢補間
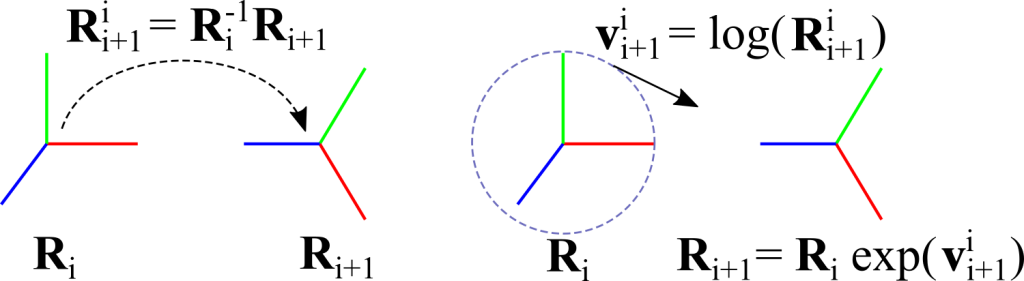
簡単な例として二つの姿勢\({\bf R}_i\)と\({\bf R}_{i+1}\)があったとき,この姿勢間の補間\({\tilde {\bf R}}^i_{i+1}(t)\)を与えることを考える.まず,\({\bf R}_i\)から見た\({\bf R}_{i+1}\)の相対姿勢\({\bf R}^i_{i+1} = {\bf R}^{-1}_i{\bf R}_{i+1}\)を考え,このLogmapを取ることで\({\bf R}_i\)の接空間における姿勢変換速度\({\bf v}^i_{i+1} = \log ( {\bf R}^i_{i+1} )\)を求める.Expmapを使い,この\({\bf v}^i_{i+1}\)を\(t \in [0, 1]\)でスケーリングしながら\({\bf R}_i\)に加えることで\({\bf R}_i\)と\({\bf R}_{i+1}\)間のスムーズな補間を得ることができる:\({\tilde {\bf R}}^i_{i+1}(t) = {\bf R}_i \exp ({\bf v}^i_{i+1} t)\).
上式を使うことで,\({\bf R}_i\)の次元(2次元,3次元)や,回転に加えて並進・スケーリングを考慮するか(SO3, SE3, Sim3)に関わらず全く同じ方式で補間することができ,微分も比較的容易に求めることができる.このように数式的にエレガントで実装が容易なのもExpmap/Logmap補間を使う大きな要因の一つである.
これで最も単純な2姿勢間の補間が与えられたが,実際に補間を行う際には,1) 回転・並進を独立に扱うか,2) どのように姿勢をブレンドするか,の二点を考慮する必要がある.
回転・並進の独立性
Expmap/Logmapを使うことでSO3・SE3の区別なく補間を行うことができると書いたが,これを使って直接SE3空間上でExpmap補間を行うか,回転成分(SO3)のみExpmap補間を使い並進成分は別で線形補間するか,という二つの方法が考えられる.直接SE3空間上でExpmap補間する場合は回転と並進が同時に作用するように補間が行われるが,回転・並進を分ける場合はこれらが独立に作用するように補間が働く.
例えば,野球のボールを投げた時のように物体がまっすぐ進みながら空転する場合を考える.このとき物体の回転と並進は独立して行われるため,回転・並進を分けて補間した方が良い補間結果が得られる.

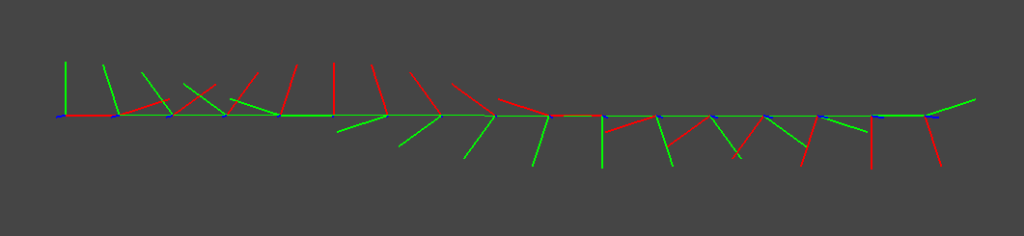
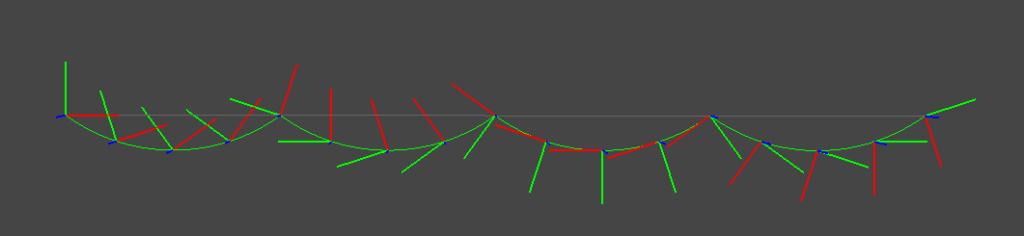
一方で,車のハンドルを切りながら前進した場合のように移動量が回転状態に対する局所的な速度で与えられる場合,直接SE3空間上でExpmap補間を行うことで良い補間結果が得られる.

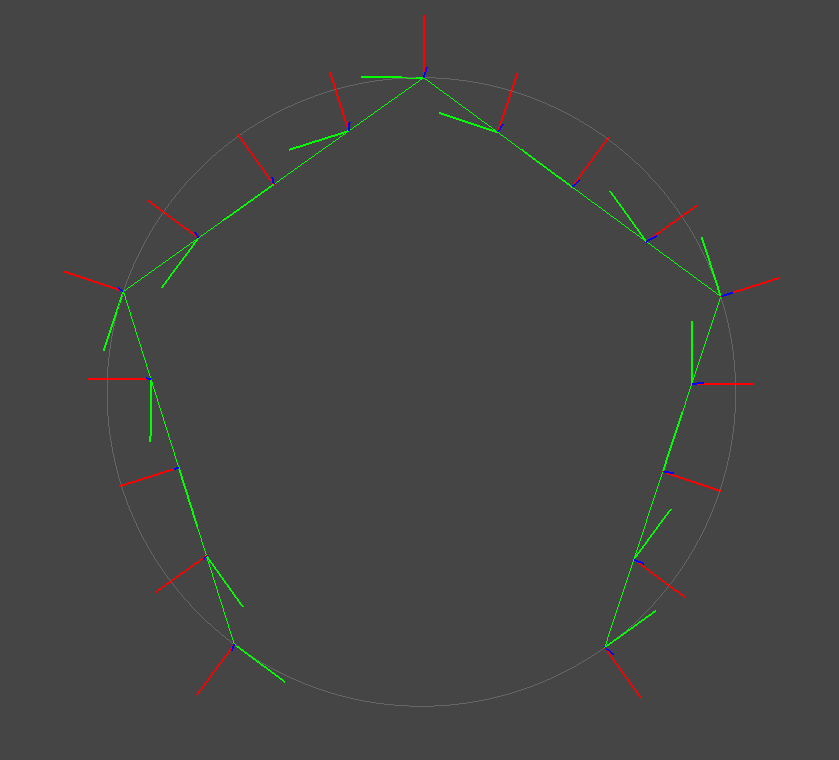

どちらの方が良いかは一概には言えないため,想定する姿勢運動に応じて適切な方式を選ぶ必要がある.例えば自由運動する物体を想定する場合には回転・並進を独立して補間し,車や飛行機のように移動方向が物体前方に限られる運動に関してはSE3補間を使うと良いだろう.実際の運用上は姿勢が細かく与えれらればそれほど大きな差異にはならないため,個人的には実装が簡易になるSE3補間を多用しがちではある.
姿勢のブレンド方式 (Cubic Hermite Spline & Cubic B-Spline)
上の図で見て取れるように,単純な2姿勢間の線形補間では区間が切り替わるときに運動が不連続になってしまう.最適化に適した連続な補間を得るためによく使われるのがn次スプライン補間であり,特にC2連続になる3次スプラインが重要である.一言に3次スプライン補間と言っても多様な方式があるが,実装が容易で特に多用されるものにCubic HermiteスプラインとCubic Bスプラインがある.どちらも与えられた姿勢系列に沿った補間を与えるが,Cubic Hermiteスプラインは厳密に各姿勢を通る補間を与えるのに対して,Bスプラインは各姿勢を通らないスムージングされた補間を与える.
Cubic Hermiteスプライン
2つの制御点\({\bf p}_i, {\bf p}_{i+1}\)間のCubic Hermite補間は以下の式で与えられる(https://en.wikipedia.org/wiki/Cubic_Hermite_spline):
\( \tilde{{\bf p}}^i_{i+1}(t) = (2t^3 – 3t^2 + 1) {\bf p}_i + (t^3 – 2t^2 + t) {\bf m}_i + (-2 t^3 + 3 t^2) {\bf p}_{i+1} + (t^3 – t^2) {\bf m}_{i+1} .\)
ここで\({\bf m}_i, {\bf m}_{i+1}\)は各制御点におけるスプライン制御パラメータ (変化速度)であり,Catmull-Rom方式では以下で与えられる:
\( {\bf m}_k = \frac{1}{2} ( {\bf p}_{k+1} – {\bf p}_{k-1} ) .\)
まず,Expmap補間を適用可能にするために\({\tilde {\bf p}}^i_{i+1}(t)\)を以下のように\({\bf p}_i\)に対する相対的な値に変形する:
\( {\tilde {\bf p}}^i_{i+1}(t) = {\bf p}_i + (t^3 – 2t^2 +t) {\bf m}_i + (-2 t^3 + 3 t^2) ({\bf p}_{i+1} – {\bf p}_{i}) + (t^3 – t^2) {\bf m}_{i+1} .\)
ここで,最初に説明したExpmap/Logmap補間の例と同様に,Logmapによる姿勢間の変換速度の算出とExpmapによる積算を適用すると姿勢のCubic Hermite補間が以下のように得られる(注:exp積算の順番はもしかしたら違うかも?):
\(
\begin{align*}
{\tilde {\bf R}}^i_{i+1} (t) &= {\bf R}_i \exp \left( (t^3 – 2t^2 + t) {\bf m}_i \right) \exp \left( (-2 t^3 + 3 t^2) \log ( {\bf R}_i^{-1} {\bf R}_{i+1} ) \right) \exp \left( (t^3 – t^2) {\bf m}_{i + 1} \right), \\
{\bf m}_k &= \frac{1}{2} \log \left( {\bf R}_{k-1}^{-1} {\bf R}_{k+1} \right) .
\end{align*}
\)
Cubic Bスプライン
時刻\(t\)が2つの制御点\({\bf p}_i, {\bf p}_{i+1}\)の間にあるとき,3次Bスプライン補間は以下の式のように近傍の制御点の単純な合成で与えられる (Sec 2.2.1 in https://www.robots.ox.ac.uk/~mobile/Theses/StewartThesis.pdf):
\(
\begin{align*}
\tilde{{\bf p}}(t) &= \beta_{i-1}(t) {\bf p}_{i-1} + \beta_{i}(t) {\bf p}_{i} + \beta_{i+1}(t) {\bf p}_{i+1} + \beta_{i+2}(t) {\bf p}_{i+2}, \\
\beta_{i-1}(t) &= \frac{1}{6} (1 – 3t + 3t^2 – t^3), \\
\beta_{i}(t) &= \frac{1}{6} (4 – 6t^2 + 3t^3), \\
\beta_{i+1}(t) &= \frac{1}{6} (1 + 3t + 3t^2 -3t^3), \\
\beta_{i+2}(t) &= \frac{1}{6} (t^3).
\end{align*}
\)
Cubic Hermiteの時と同様にExpmap補間を行うため,それぞれの\({\bf p}_k\)を一つ前の\({\bf p}_{k – 1}\)に対する相対量で表し,\(\tilde{{\bf p}}(t)\)を以下のように変形する(Sec. 2.2.2):
\(
\begin{align*}
\tilde{{\bf p}}(t) &= \tilde{\beta}_{i-1} {\bf p}_{i-1}+ \tilde{\beta}_{i}(t) ({\bf p}_{i} – {\bf p}_{i-1})+ \tilde{\beta}_{i+1}(t) ({\bf p}_{i+1} – {\bf p}_{i}) + \tilde{\beta}_{i+2}(t) ({\bf p}_{i+2} – {\bf p}_{i+1}), \\
\tilde{\beta}_{i-1}(t) &= 1, \\
\tilde{\beta}_{i}(t) &= \frac{1}{6} (5 + 3t – 3t^2 + t^3), \\
\tilde{\beta}_{i+1}(t) &= \frac{1}{6} (1 + 3t + 3t^2 – 2t^3), \\
\tilde{\beta}_{i+2}(t) &= \frac{1}{6} t^3.
\end{align*}
\)
これに対してExpmap/Logmap補間を適用すると,以下のように姿勢の補間式が与えられる:
\(
\tilde{\bf R}(t) = {\bf R}_{i-1}
\exp \left( \tilde{\beta}_{i} \log ( {\bf R}_{i-1}^{-1} {\bf R}_{i} ) \right)
\exp \left( \tilde{\beta}_{i+1} \log ( {\bf R}_{i}^{-1} {\bf R}_{i+1} ) \right)
\exp \left( \tilde{\beta}_{i+2} \log ( {\bf R}_{i+1}^{-1} {\bf R}_{i+2} ) \right)
\)
補間例
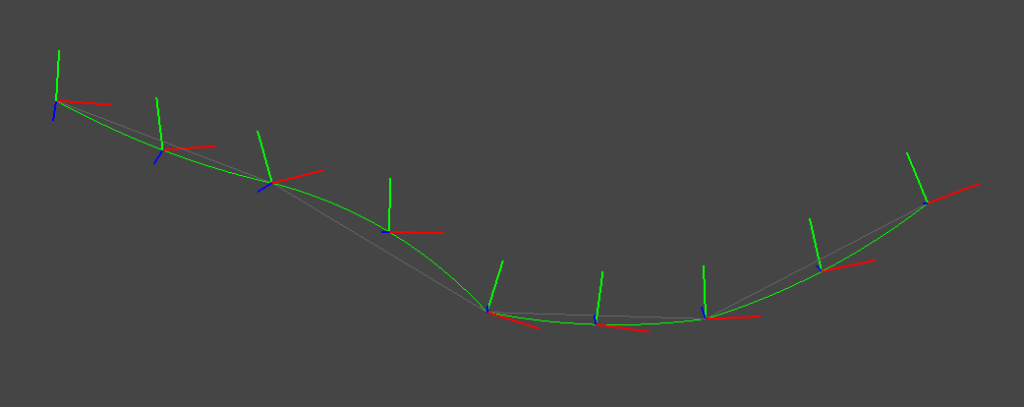
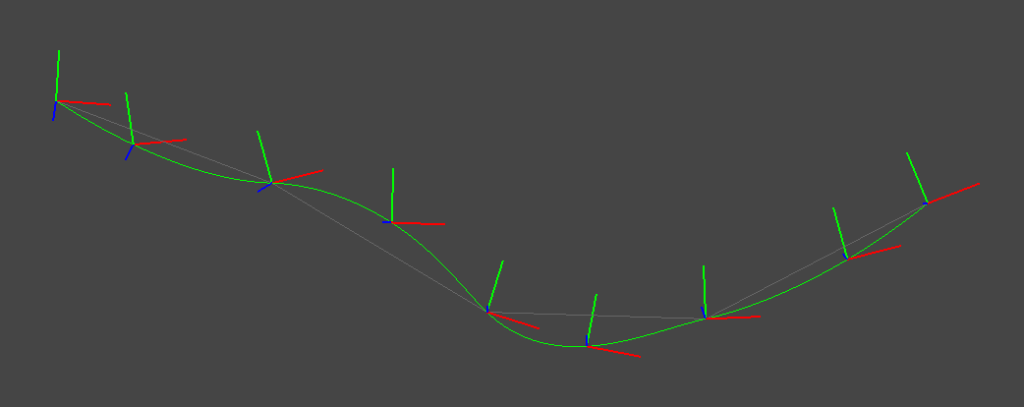
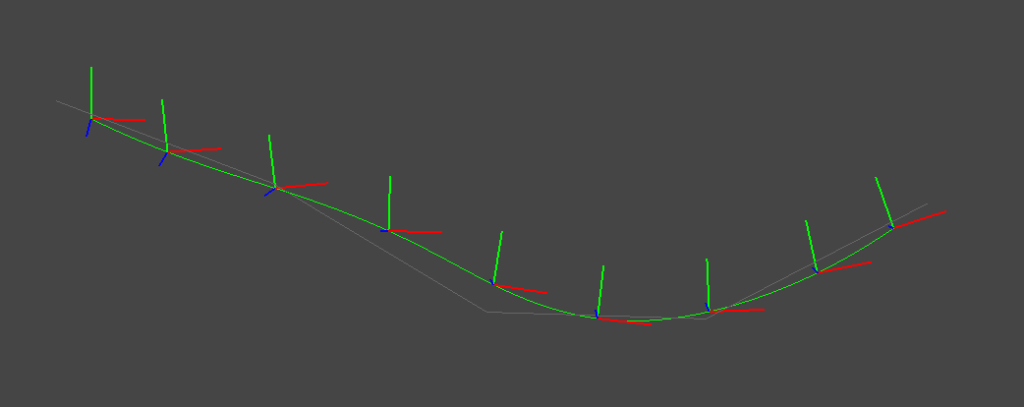
実際に,ランダムな姿勢系列に対して,線形補間・Cubic Hermiteスプライン補間・Cubic Bスプライン補間を適用すると以下のような補間結果が得られる.
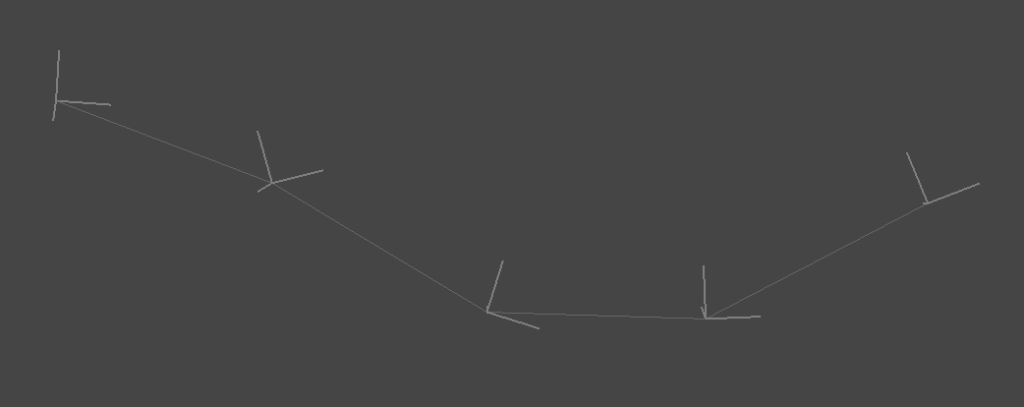
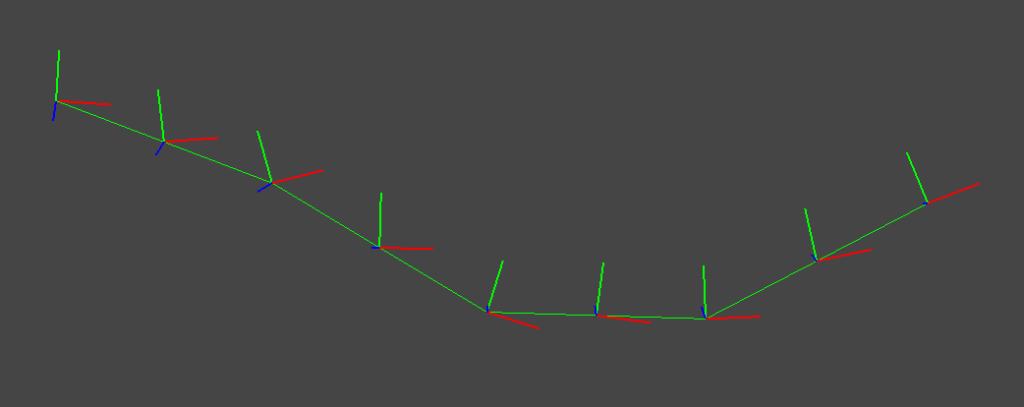
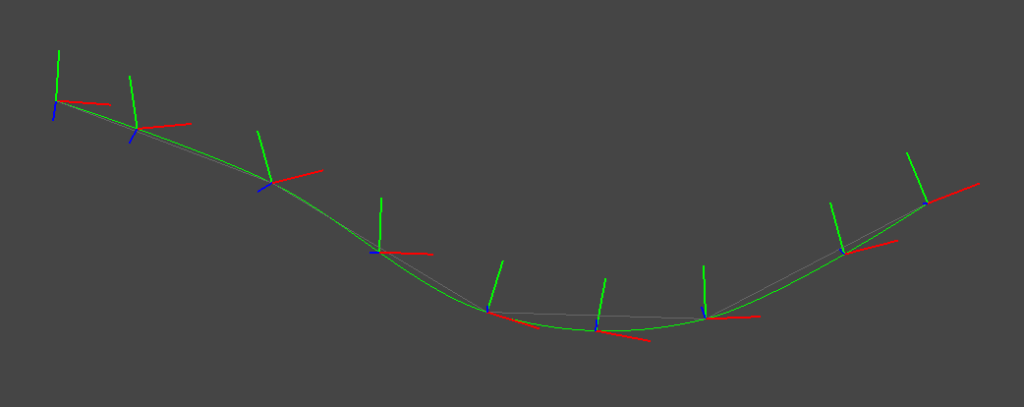

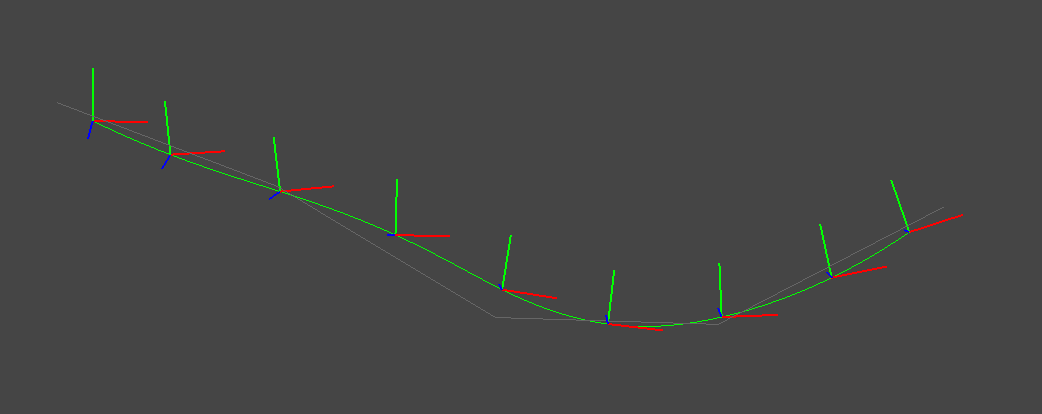
2種類のスプライン補間はそれぞれ連続した運動が得られていることが見て取れる.また,Cubic Hermiteスプラインは補間結果が制御点を必ず通っているのに対して,Bスプラインは制御点を通らない補間になっていることがわかる.なお,上図では回転・並進を分離した補間 (SO3 expmap + linear Trans)を行っているが,SE3空間上で回転・並進を同時に作用する補間 (SE3 expmap)を行うと下図のような結果になる.
あとがき
今回は詳細な姿勢補間について実例を交えながら説明した.より直感的な理解を助けるようにブラウザ上で動作するような補間デモを作ろうと思っていたが,THREE.jsの行列演算機能が弱すぎてjavascript上での実装を今回は断念した.もうちょっと実用に耐えるjs用の線形代数ライブラリが見つかったらまたデモプログラムの実装をやってみようと思う.
コメント